Algebra

Functions and Graphing

Let’s begin by going over what a function is. At its simplest level, a function will take in a number, apply some operation to it, and output another number. Let’s go over notation first.

Functions are denoted by \(f(x) = \text{Some function}\). Note that it doesn’t have to be f(x), it could be \(g(x)\), \(h(x)\), or any other letter. However, it’s usually \(f(x)\). Some example of functions are:

\[f(x) = x^3+2\\ g(x) = \frac{2}{x}-3\\ h(x) = \sqrt{x}\]

The input here is the \(x\) in parentheses after the \(f\), \(g\), and \(h\). When inputting a number into the x value, we substitute every x inside the function for that number. For example:

\[\begin{align*} f(x) &= x^3+2\\ f(5) &= 5^3+2\\ f(5) &= 127 \end{align*}\] \[\begin{align*} g(x) &= \frac{2}{x}-3\\ g(0.5) &= \frac{2}{0.5}-3\\ g(0.5) &= 1 \end{align*}\]

That’s how we write functions algebraically. We can also visualize them using tables. Consider the following table for the function \(f(x) = 3x+1\):

\(x\)	\(f(x\))
-2	-5
-1	-2
0	1
1	4
2	7

Or, we can use graphs. Functions on graphs are very useful and common. This is the graph for the same function \(f(x) = 3x+1\). On the x-axis (big horizontal line), lies the value of an x value (an input to the function). On the y-axis (big vertical line), lies the corresponding f(x) value. For example, 3 units to the right of the origin (the origin is where the two axes cross), the y value is 10, because \(f(3) = 3(3)+1= 10\).

An important note about functions: when inputting a number into a function, the function should always return either 1 or 0 numbers. In other words, inputting a number into a function can never give 2 (or more) results. For example, the following graph is not a function:

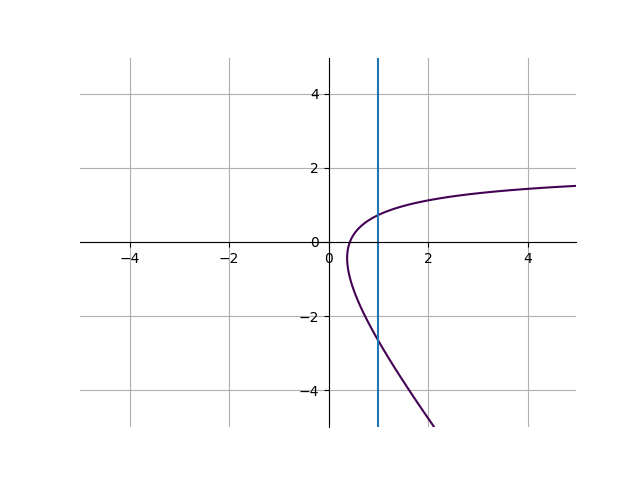
because at \(x=1\), there are two y values. You can use something called the vertical line test to test if a function on a graph is actually a function. If you can make at least 1 vertical line on the graph that crosses the function at least twice, that is automatically not a function.