Geometry
Congruency
In the last topic, we covered the fundamentals of congruence in both shapes and angles. Now, let's talk about some Proofs of Congruence.
Congruent Triangles: In order to decide whether a pair of triangles are congruent, we have to measure all of the sides and angles. But because it is really tedious to do so, we use the Triangle Congruence Criteria.
Side-Side-Side (SSS)
When all three pairs of corresponding sides are congruent, the triangles are congruent.
Proof: In \(\Delta ABC\) and \(\Delta DEF\), we're given:
$$\overline{\rm AB} \cong \overline{\rm EF}\\
\overline{\rm BC} \cong \overline{\rm ED}\\
\overline{\rm AC} \cong \overline{\rm DF}$$
Side-Angle-Side (SAS)
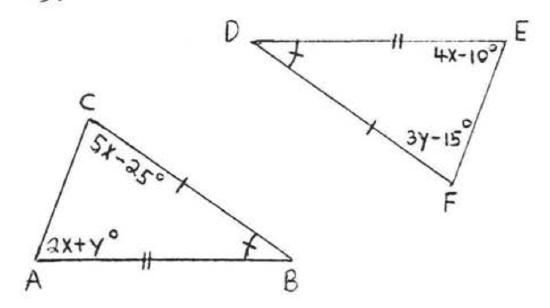
When two pairs of corresponding sides and the corresponding angles between them are congruent.
Proof: In \\(\Delta ABC\\) and \\(\Delta DEF\\), we're given:
$$\overline{\rm AB} \cong \overline{\rm DE}\\
\angle{B} \cong \angle{D}\\
\overline{\rm BC} \cong \overline{\rm DF}$$
Angle-Side Angle (ASA)

When two pairs of corresponding angles and the corresponding sides between them are congruent.
Proof: In \(\Delta ABC\) and \(\Delta DEF\), we're given:
$$\overline{\rm AB} \cong \overline{\rm DE}\\
\angle{A} \cong \angle{D}\\
\angle{B} \cong \angle{E}$$
Angle-Angle-Side (AAS)

When two pairs of corresponding angles and one pair of corresponding sides (not between the angles) are congruent.
Proof: The interior angle measures of a triangle have a total sum of \(180^\circ\) Once we know any two angle measures, we can calculate the third.
When we know all of the angle measures, we can use the two that are adjacent to the known side, and then apply the ASA criteria.
Hypotenuse Leg (HL)

When the hypotenuses and a pair of corresponding sides of right triangles are congruent, the triangles are congruent.
Proof: Using the Pythaegorean Theorem, we can find the third side of the triangle, if we already know two sides.
$$(\text{Hypotenuse})^2 = (\text{Leg One})^2 + (\text{Leg Two})^2$$