Geometry

Analytic Geometry

In the last topic, we covered the Congruency Proofs that are used in Geometry. Now, let’s talk about some Analytic Geometry, the study of geometry with what’s known as a coordinate system. A Coordinate Plane is a 2D picture that contains points, each one having a coordinate.

Every coordinate is described with an ordered pair in the form \((x,y)\), where \(x\) represents the horizontal position, and \(y\) represents the vertical position.

First to note on a coordinate plane are the axes, or the lines infinitely long lines that run through them. Because the coordinate plane is 2-dimensional, there are 2 axes - the \(x\)-axis and \(y\)-axis. The \(x\)-axis runs horizontally and the \(y\)-axis runs vertically. At the center, where the two axes interesect, lies the point with the coordinate \((0, 0)\), a point so important it has its own name - the origin.

Points to the left of the origin have negative \(x\)-coordinates, and points to the right have positive \(x\)-coordinates. Similarly, points below the origin have negative \(y\)-coordinates, and points above the origin have positive \(y\)-coordinates.

In this image, point \(A\) is at \((4,3)\) and point \(B\) is at \((-2,-3)\). Here, \((4,3)\) and \((-2,-3)\) are the ordered pairs. At the center is the origin.

The (distance) between the points \((x_1,y_1)\) and \((x_2,y_2)\) (where \(x_1\), \(y_1\), \(x_2\), and \(y_2\) are numbers) is given by the following formula:

\[\text{Distance} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\]

This is derived from the Pythagorean Theorem. If we want to find the distance between two points, we can simply transform the two points, into a line, and then, into a right triangle. Here’s an example:

With this right triangle in place, now we can use the Pythagorean Theorem: The expression for the base is \((x_2-x_1)\) and the expression for the length is \((y_2-y_1)\). Now, we can use the formula:

\[\text{distance}^2 = (x_2-x_1)^2 + (y_2-y_1)^2\]

Solving for distance, we have

\[\text{distance} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\]

The midpoint (point directly in the middle of two other points, on the line connecting the two other points) of the points \((x_1,y_1)\) and \((x_2,y_2)\) is given by the following formula:

\[\text{midpoint} = \frac {x_1+x_2}{2}, \frac{y_1+y_2}{2}\]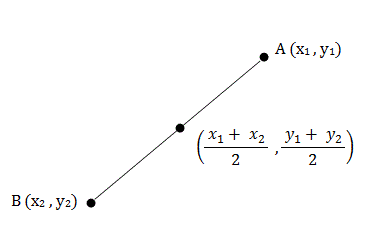

Note about parellel and perpendicular Lines: Two lines that are parallel have the same slope. Perpendicular lines have the negative reciprocal slope of the other line.