Geometry
Circles, Volume, and Surface Area
We’ve covered the fundamentals of Congruency, Proofs, and Geometry. Finally, we’ll move on to the more complicated topics of Circles, Volume, and Surface Area.
Circles
Arc of a Circle: It is basically any portion of the circumference of a circle. The circumference is the perimeter of a circle. Hence, the circumference is a full arc of the circle.
Finding the Length of an Arc:
Arc Length: The length of an arc is the distance between the start and end points of the arc.
Formula for the arc length = \((2πr)(θ/360)\), where \(r\) is the radius of the circle.
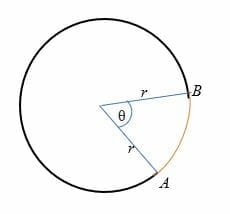
The length of the arc (drawn in red) is the distance from point A to point B.
Example: Arc \(AB\) has an angle of \(40°\) and the circle has a radius of \(7\)cm. Calculate the length of arc \(AB\).
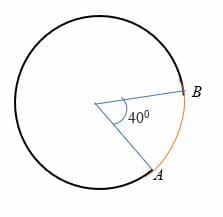
Answer: \((2π \cdot 7) \cdot (40/360)\) = \(4.884\)cm.
Area of Sector of a Circle: Space enclosed by the sector of a circle.
Formula = Area of sector of circle = \((πr^2)\) \((θ/360)\), where \(θ\) is the sector angle subtended by the arc at the center, in degrees. And, \(r\) is the radius of the circle.
Area of sector of circle = \((\frac {1}{2})\) \((r^2 θ)\), where \(θ\) is the sector angle subtended by the arc at the center, in radians. And, \(r\) is the radius of the circle.

Volume Formulas:
Volume of a Cube:
Formula = \(V = a^3\), where \(a\) is the length of an edge of the cube.
Volume of a Rectangular Prism:
Formula = \(V = whl\), where \(w\) is the width of the prism, \(h\) is the height of the prism, and \(l\) is the length of the prism.
Volume of a Cylinder:
Formula = \(V = πr^2h\), where \(r\) is the radius of the cylinder, and \(h\) is the height of the cylinder.
Volume of a Sphere:
Formula = \(V = \frac {4}{3}\) \(πr^3\), where \(r\) is the radius of the sphere.
Volume of a Cone:
Formula = \(V = πr^2h/3\), where \(r\) is the radius of the cone, and \(h\) is the height of the cone.
Volume of a Pyramid:
Formula = \(V = l * w * (\frac{h}{3})\), where \(w\) is the width of the pyramid, \(h\) is the height of the pyramid, and \(l\) is the base length of the pyramid.
Surface Area Formulas:
Surface Area of a Cube:
Formula = \(SA = 6a^2\), where \(a\) is the edge of the cube.
Surface Area of a Rectangular Prism:
Formula = \(SA = 2wh + 2wl + 2hl\), where \(w\) is the width of the prism, \(h\) is the height of the prism, and \(l\)is the length of the prism.
Surface Area of a Cylinder:
Formula = \(SA = 2πr^2 + 2πrh\), where \(r\) is the radius of the cylinder, and \(h\) is the height of the cylinder.
Surface Area of a Sphere:
Formula = \(SA = 4πr^2\), where \(r\) is the radius of the sphere.
Surface Area of a Cone:
Formula = \(SA = πr^2 + πrl\), where \(r\) is the radius of the cone, \(h\) is the height of the cone, and \(l\) is the slant height of the cone.