Precalculus
Exponentials and Logarithms
Let’s discuss another umbrella of functions, exponential functions. An exponential function is a function written in the form of
\[f(x)=ab^x\]The important part here is how \(x\) is in the exponent - this key part is what makes it an exponential function. This is in contrast to polynomial functions, where \(x\) is in the base. Here is a graph of the function \(2^x\):
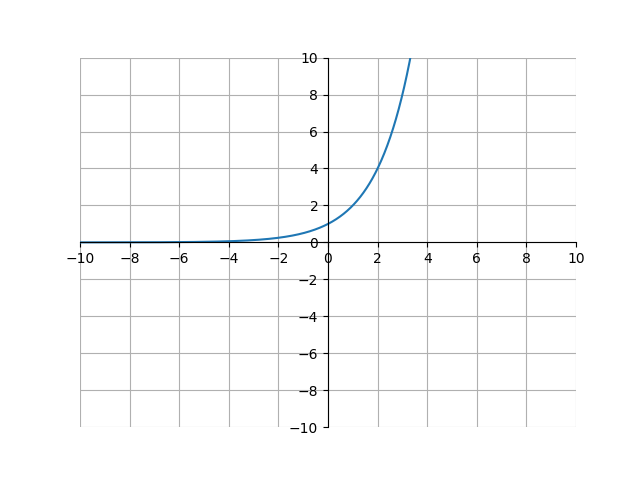
The first thing to notice is that \(2^x\) grows very fast. This is because the y-value doubles after each unit step in the x direction. This is because every time we add 1 to the x-value, the y value will be multiplied by 2 another time:
\[\begin{align*} 2^3 &= 2\cdot2\cdot2 = 8 \\ 2^4 &= 2\cdot2\cdot2\cdot2 = 16 \\ 2^5 &= 2\cdot2\cdot2\cdot2\cdot2 = 32 \end{align*}\]Another thing to notice is what happens when \(x=0\). Any number raised to the 0th power is 1, meaning
\[f(0)=ab^0\] \[f(0)=a\cdot1\] \[f(0)=a\]Thus, the y-intercept of an exponential function in the form \(f(x)=ab^x\) is always \(a\). We can verify this by graphing some more exponential functions:
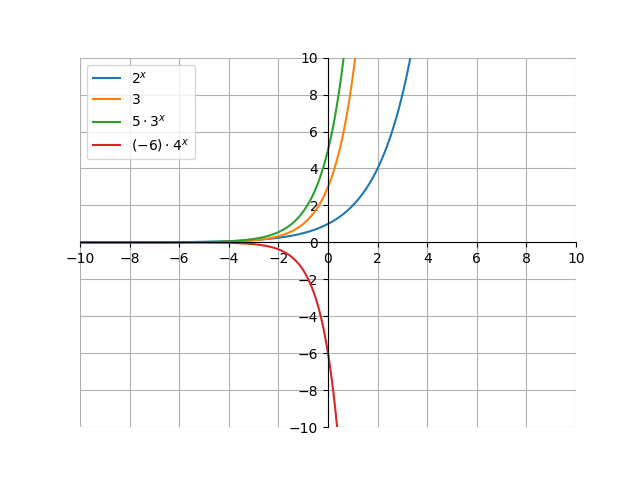
Exponential equations come up a lot in the real world. For example, imagine 5 bacteria on a petri dish. Every hour, the number of bacteria doubles. This means that the number of bacteria follow the function \(B(t)=5\cdot2^t\), with \(t\) being the number of hours.
Now, let’s talk about solving equations with exponentials. Suppose we wanted to solve the equation \(3^x=10\), how would we go about doing it? \(3^2\) is 9 and \(3^3=27\), so we know the answer is very close to 2, but we do not have an exact form. Fortunately, we can use a logarithm.
A logarithm is the inverse function of the exponential, in the same way that multiplication is the inverse of division and subtraction is the inverse of addition.
A logarithm looks like:
\[g(x)=\log_bx\]Here, \(b\) is the base of the logarithm. Logarithms are just a family of functions, and \(b\) is a parameter. We can relate exponential functions and logarithms by solving an equation:
\[3^x=10\]Let’s apply a logarithm here. The base of the exponential is \(3\), so let’s apply a logarithm with base 3 to both sides.
\[\log_{3}{3^x}=\log_{3}{10}\]Here is the key part of a logarithm - a logarithm of a base next to an exponential with the same base will cancel out, leaving only the power. In general:
\[\log_{b}{b^a} = \cancel{\log_{b}}\cancel{b}^a = a\]This means that
\[\cancel{\log_{3}}\cancel{3}^x=\log_{3}{10}\] \[x=\log_{3}{10}\]Which, if you plug into a calculator, you will find is approximately \(2.096\). Here is a handy diagram that might help you relate exponentials and logarithms:
\[\log_b(a)=c \Leftrightarrow b^c=a\]When we graph logarithms, we should remember that logarithms are just an inverse of exponentials. So, to graph a logarithmic function, we flip the corresponding exponential function over the line \(y=x\). This means that
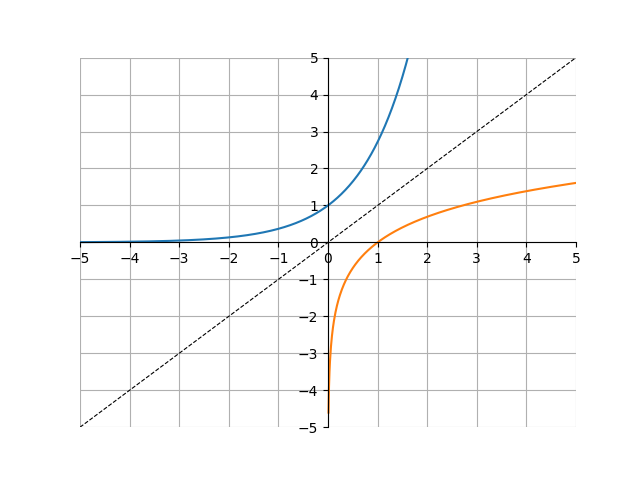
In general, the graph of a logarithm will look like a sideways exponential, with a vertical asymptote at \(x=0\), just like how the graph of an exponential has a horizontal asymptote at \(y=0\).
Now, let’s discuss some properties of logarithms. There are four main properties to know. Let’s start with the first one, the product rule law, which says
\[\log_{b}{M\cdot N}\ = \log_{b}{M}+\log_{b}{N}\]For example, \(\log_{2}{14} = \log_{2}{2\cdot6} = \log_{2}{2}+\log_27 = 1+\log_27\). This works because it is a parallel to the product rule for exponents law.
The second law is the quotient rule law. This says
\[\log_{b}{\frac{M}{N}} = \log_{b}{M} - \log_{b}{N}\]For example, \(\log_{5}{\frac{2}{5}}=\log_{5}{2}-\log55=\log_52-1\). This law works because it is parallel to the quotient rule for exponents law.
The third law is the power rule law. This says
\[\log_{b}{a^c}=c\cdot\log_{b}{a}\]For example, \(\log_{3}{32} = \log_{3}{2^5} = 5\log{3}{2}\). This law works because it is just the product rule repeated \(c\) times.
The fourth law is the change of base law. This law says that
\[\log_{b}{a} =\frac{\log_da}{\log_db}\]\(d\) can be any number. For example, \(\log_27 = \frac{\log_37}{\log_32} = \frac{\log_47}{\log_42} = \frac{\log_57}{\log_52}\)